Improving the prediction of effective lens position for intraocular lens power calculations
Abstract
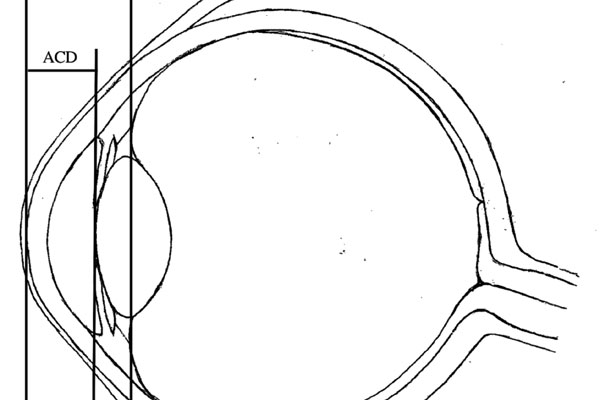
Purpose: Achieving the desired post-operative refraction in cataract surgery requires accurate calculations for intraocular lens (IOL) power. Latest-generation formulae use anterior-chamber depth (ACD)—the distance from the corneal apex to the anterior surface of the lens—as one of the parameters to predict the post-operative IOL position within the eye, termed the effective lens position (ELP). Significant discrepancies between predicted and actual ELP result in refractive surprise. This study aims to improve the predictability of ELP. We hypothesise that predictions based on the distance from the corneal apex to the mid-sagittal plane of the cataractous lens would more accurately reflect the position of the principal plane of the non-angulated IOL within the capsular bag. Accordingly, we propose that predictions derived from ACD + ½LT (length thickness) would be superior to those from ACD alone.
Design: Retrospective cohort study, comparing ELP predictions derived from ACD to a
proposed prediction parameter.
Method: This retrospective study includes data from 162 consecutive cataract surgery cases, with posterior-chamber IOL (AlconSN60WF) implantation. Pre- and postoperative biometric measurements were made using the IOLMaster700 (ZEISS, Jena, Germany). The accuracy and reliability of ELP predictions derived from ACD and ACD + ½LT were compared using software-aided analyses.
Results: An overall reduction in average ELP prediction error (PEELP) was achieved using the proposed parameter (root-mean-square-error [RMSE] = 0.50 mm), compared to ACD (RMSE = 1.57 mm). The mean percentage PEELP, comparing between eyes of different axial lengths, was 9.88% ± 3.48% and −34.9% ± 4.79% for predictions derived from ACD + ½LT and ACD, respectively. A 44.10% ± 5.22% mean of differences was observed (p < 0.001).
Conclusion: ACD + ½LT predicts ELP with greater accuracy and reliability than ACD alone; its use in IOL power calculation formulae may improve refractive outcomes.
References
Norrby SJ. Sources of error in intraocular lens power calculation. Cataract Refract Surg. 2008;34(3):368-376.
Muthappan V, Paskowitz D, Kazimierczak A, Jun AS, Ladas J, Kuo IC. Measurement and use of postoperative anterior chamber depth of fellow eye in refractive outcomes. J Cataract Refract Surg. 2015;41(4):778-784. doi:10.1016/j.jcrs.2014.08.034.
Rosen AM, Denham DB, Fernandez V, et al. In vitro dimensions and curvatures of human lenses. Vis Res. 2006;46(6-7):1002-1009.
Jones CE, Atchison DA, Pope JM. Changes in lens dimensions and refractive index with age and accommodation. Optom Vis Sci. 2007;84(10):990-995.
Richdale K, Bullimore MA, Zadnik K. Lens thickness with age and accommodation by optical coherence tomography. Ophthalmic Physiol Opt. 2008;28(5):441-447.
Sheard R. Optimising biometry for best outcomes in cataract surgery. Eye. 2014;28(2):118-125.
Ong K, Feng L. Prevalence of variation in predicted refraction between different intraocular lens formulae. Asian J Opthalmol. 2018;16:60-61.
Abulafia A, Barrett GD, Rotenberg M, et al. Intraocular lens power calculation for eyes with an axial length greater than 26.0 mm: comparison of formulas and methods. J Cataract Refract Surg. 2015;41(3):548-556. doi:10.1016/j.jcrs.2014.06.033.
Wong RS, Ong K. Influence of anterior chamber depth on postoperative refractive outcome in Chinese eyes. Asian J Opthalmol. 2018;16:79-85.
D’Agostino RB. Tests for normal distribution. In: D’Agostino RB, Stepenes MA, eds. Goodness-Of-Fit Techniques. Boca Raton, FL: CRC Press.
Aristodemou P, Knox Cartwright NE, Sparrow JM, Johnston RL. Intraocular lens formula constant optimization and partial coherence interferometry biometry: refractive outcomes in 8108 eyes after cataract surgery. J Cataract Refract Surg. 2011;37(1):50-62.
Sanders DR, Retzlaff J, Kraff MC. Comparison of the SRK II formula and other second generation formulas. J Cataract Refract Surg. 1988;14(2):136-141.
Sahin A, Hamrah P. Clinically relevant biometry. Curr Opin Ophthalmol. 2012;23(1):47-53.
Haigis W. User group for laser interference biometry. http://www.augenklinik.uni-wuerzburg.de/ulib/czm/dload.htm. Accessed 9 September 2013.
Dubbelman M, Van der Heijde GL. The shape of the ageing human lens: curvature, equivalent refractive index and the lens paradox. Vision Research. 2001;41(14):1867-1877.
Olsen T. Improved accuracy of intraocular lens power calculation with the Zeiss IOLMaster. Acta Ophthalmol Scand. 2007;85(1):84-87.
Copyright (c) 2020 Juanita Noeline Chui, Keith Ong

This work is licensed under a Creative Commons Attribution 4.0 International License.
Authors who publish with this journal agree to the following terms:
- Authors retain copyright and grant the journal right of first publication, with the work twelve (12) months after publication simultaneously licensed under a Creative Commons Attribution License that allows others to share the work with an acknowledgement of the work's authorship and initial publication in this journal.
- Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the journal's published version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgement of its initial publication in this journal.
- Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work (See The Effect of Open Access).


